- Тема 9. Характеристика размеров и структуры социально-экономических явлений
- Задания по статистике по структурным средним
- Задача №1 . Нахождение моды и медианы для интервального ряда
- Задача №2. Нахождение моды и медианы для дискретного ряда.
- Теория для решения данных задач. Формулы для расчета моды и медианы
Тема 9. Характеристика размеров и структуры социально-экономических явлений
1. Имеются данные по двум предприятиям:
| № предприятия | Доля экспорта в товарной продукции | Стоимость экспортной продукции, тыс. руб. |
| 1 | 0,25 | 800,0 |
| 2 | 0,15 | 900,0 |
Какую формулу необходимо использовать для определения средней доли экспортной продукции по двум предприятиям:
1) среднюю арифметическую простую;
2) среднюю арифметическую взвешенную;
3) среднюю гармоническую взвешенную.
2. Годовой план по производству продукции предусматривал увеличение ее объема на 8%. Фактически план перевыполнен на 2,8%. На сколько процентов, увеличился объем продукции по сравнению с прошлым годом:
3. Акционерное общество планировало снизить себестоимость продукта на 3% в отчетном году по сравнению с предыдущим годом. Фактически себестоимость изделия возросла на 2% в отчетном году по сравнению с предыдущим годом. Определите, на сколько процентов был выполнен план по снижению себестоимости изделия в отчетном году:
4. Укажите правильный вывод, если средняя арифметическая величина прибыли по ряду распределения предприятий отрасли в отчетном году составила 120 млн. руб:
1) Наиболее часто предприятия отрасли имели прибыль в размере 120 млн. руб.;
2) Половина предприятий отрасли имела прибыль 120 млн. руб. и ниже, а другая половина предприятий отрасли 120 млн. руб. и выше;
3) Средний размер прибыли предприятий отрасли, составил 120 млн, руб.
5. Предприятие поставляет продукцию в три страны. Цена поставки единицы изделия в первую страну — 85 долл., во вторую — 100 долл., в третью — 118 долл. Средняя цена поставляемой на экспорт продукции составляет 105,8 долл. Каков удельный вес поставок в третью страну, если доля поставок в первую составляет 18%:
6. База сравнения (основание) – это:
1) величина, с которой производят сравнение;
2) величина, которая сравнивается;
3) величина, получаемая в результате сравнения.
7. Численность студентов института по формам обучения составляет:
дневная — 2130 чел.;
вечерняя — 3030 чел.
Какие виды относительной величины можно исчислить?
8. Средняя величина – это обобщающий показатель:
1) характеризующий различие индивидуальных значений признака у разных единиц совокупности в один и тот же период времени;
2) характеризующий совокупность однородных явлений по какому-либо варьирующему признаку и отражающий типичный уровень признака в данной совокупности;
3) выражающий абсолютные уровни общественных явлений и процессов.
9. Модой в ряду распределения является:
1) значение признака, делящее ряд ранжированных значений на две равные части;
2) наибольшее значение признака;
3) значение признака, которое встречается чаще других.
10. Цехом произведены бракованные детали в двух партиях: в первой партии – 5 шт., что составило 3,4% от общего числа деталей; во второй партии – 10 шт. или 6,1% от общего числа деталей. Определить средний процент бракованных деталей.
11. Цехом произведены бракованные детали в двух партиях: в первой партии – 5 шт., что составило 4,0% от общего числа деталей; во второй партии – 10 шт. или 5,0% от общего числа деталей. Средний процент бракованных деталей составит:
12. Портфель состоит из акций трех компаний. Их доходность равна соответственно 15, 20 и 22%, а доля в портфеле – 10, 70 и 20%. Следовательно, средняя доходность портфеля составит:
13. Относительные величины, характеризующие долю собственного и долю заемного капитала в общей величине капитала фирмы относятся к величинам:
14. Средняя цена товара по двум пунктам его реализации, рассчитанная по следующим данным
| Пункт реализации | Цена товара, руб. | Стоимость реализованного товара, руб. |
| №1 №2 | 15 22 | 18000 16500 |
15. Медиана – это значение признака в совокупности:
2) наиболее часто встречающееся;
3) находящееся в середине ранжированного ряда распределения.
16. Средняя является надежной характеристикой в:
1) однородных совокупностях;
2) неоднородных совокупностях;
3) в любых совокупностях.
17. Известны следующие данные:
| Число дней прогулов | 1 | 2 | 3 | 4 | 5 |
| Количество рабочих | 5 | 9 | 3 | 2 | 1 |
Мода по приведенным данным составляет:
18. Укажите правильный вывод по ряду распределения предприятий отрасли по величине прибыли, если Ме =140 млн. руб.
1) Наиболее часто предприятия отрасли имели прибыль в размере 140 млн. руб.
2) Половина предприятий отрасли имела прибыль 140 млн. руб. и ниже, а другая половина предприятий отрасли 140 млн. руб. и выше.
3) Средний размер прибыли предприятий отрасли составил 140 млн. руб.
19. Предприятие перевыполнило план реализации продукции в отчетном году на 1,4%. Увеличение реализации продукции в отчетном году по сравнению с прошлым годом составило 2,0%.
Это означает, что плановое задание по росту объема реализации продукции равнялось:
20. Отдел маркетинга фирмы реализует продукцию «А» по двум каналам распределения:
Доля первого канала распределения в общей сумме выручки от реализации равна:
21. Имеются данные о производственном стаже рабочих цеха:
| Стаж в годах | До 5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число рабочих | 5 | 15 | 20 | 8 | 6 |
Средний стаж рабочих цеха:
22. Туристическая фирма планировала увеличить объем реализации путевок в текущем году на 3% по сравнению с прошлым годом. Относительная величина динамики реализации путевок составила 1,05. Насколько процентов выполнен план турфирмой по объему реализации путевок:
23. По двум предприятиям, вырабатывающим однородную продукцию, имеются следующие данные:
| Номер предприятия | Общая сумма затрат, тыс. руб. | Себестоимость единицы, руб. |
| 1 | 500,0 | 25,0 |
| 2 | 280,8 | 23,4 |
Средняя себестоимость продукции в целом по двум предприятиям:
24. С какой целью рассчитывается коэффициент вариации:
1) охарактеризовать структуру явления;
2) охарактеризовать форму распределения признака;
3) для сравнения колеблемости различных признаков в одной и той же совокупности.
25. Туристическая фирма планировала увеличить объем реализации путевок в текущем году на 2,5% по сравнению с прошлым годом. Относительная величина выполнения плана по реализации путевок в текущем году составила 0,988. На сколько процентов изменился объем реализации путевок в текущем году по сравнению с прошлым годом:
26. Что означает относительная величина координации?
1) отражает результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду (или моменту) времени, но к разным объектам или территориям;
2) представляет собой результат сопоставления разноименных показателей;
3) отражает соотношение численности двух частей единого целого.
27. Определить средний размер двух видов вклада в банке в октябре:
Выбрать правильные ответы, приведенные в следующей последовательности:
1) средний размер вклада по двум видам в октябре.
28. Общая дисперсия по депозитным вкладам предприятий – клиентов коммерческого банка (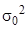 
) составила 17,19; средняя внутригрупповая дисперсия составила 5,56. Определите долю (в %) систематической вариации в общей вариации депозитных вкладов.
29. Показателем центра распределения вариационного ряда является:
1) относительный показатель асимметрии;
3) средняя арифметическая.
30. Медиана может быть определена:
1) по гистограмме;
3) по полигону распределения.
31. Для сравнительной оценки вариации и характеристики однородности совокупности наиболее часто используется:
1) среднее линейное отклонение;
2) относительное квартильное отклонение;
3) коэффициент вариации.
32. Межгрупповая дисперсия характеризует вариацию признака под влиянием:
1) всех факторов;
2) случайных факторов;
3) фактора, положенного в основу группировки.
33. Каково предельное значение коэффициента вариации при оценке однородной совокупности:
34. В обобщающие показатели вариационного ряда не входят:
1) показатели центра распределения;
2) показатели степени вариации;
3) показатели плотности распределения.
35. Вариацию, обусловленную влиянием случайных факторов признака, характеризует:
1) межгрупповая дисперсия;
2) общая дисперсия;
3) средняя из внутригрупповых дисперсий.
36. Величина общей дисперсии характеризует вариацию признака под влиянием:
1) факторного признака;
2) всех факторов;
3) неучтенных факторов.
37. По совокупности, состоящей из 50 единиц, известны: средняя арифметическая 57; сумма квадратов индивидуальных значений признака 166500. Определить, достаточно ли однородна изучаемая совокупность.
2) нельзя определить;
38. Средний размер реализованной коммерческой организацией женской обуви составил 38, мода – 36, медиана – 37. Это означает, что распределение проданной женской обуви по размеру характеризуется:
1) левосторонней асимметрией;
2) правосторонней асимметрией;
3) данные не позволяют сделать вывод.
39. Коэффициент вариации работников предприятия по размеру полученной ими премии за отчетный год составил 12,5%. Укажите правильный вывод.
1) Совокупность работников предприятия по размеру полученной ими премии за год является совершенно однородной.
2) Распределение работников по размеру полученной ими премии за год не подчиняется закону нормального распределения.
3) Совокупность работников предприятия по размеру полученной ими премии в IV квартале года неоднородна.
40. Укажите правильный вывод по ряду распределения предприятий отрасли по величине прибыли в году, если Ме=120 млн. руб.
1) Наиболее часто предприятия отрасли в году имели прибыль в размере 120 млн. руб.
2) Половина предприятий отрасли имела прибыль 120 млн. руб. и ниже, а другая половина предприятий отрасли 120 млн. руб. и выше.
3) Средний размер прибыли предприятий отрасли составил 120 млн. руб.
41. Средний стаж рабочих 6 лет. Коэффициент вариации 20%. Чему равняется дисперсия стажа работы:
42. Общая дисперсия признака 12.1 ед. Межгрупповая дисперсия 9 ед. Чему равняется средняя из групповых дисперсий:
43. По совокупности из 700 ед. при оценке влияния распространяемой в СМИ рекламы на спрос потребителей межгрупповая дисперсия составила 6280,1, средняя из внутригрупповых дисперсий — 2398,0. Оценить степень изменчивости спроса под влиянием прочих факторов.
1) доля вариации спроса потребителей под влиянием прочих факторов составила 27,63%;
2) доля вариации спроса потребителей под влиянием прочих факторов составила 72,37%;
3) доля вариации спроса потребителей под влиянием прочих факторов составила 38,13%.
44. Определить дисперсию альтернативного признака и выбрать правильный ответ на основе следующих данных: на 10000 человек населения района приходится 4500 мужчин и женщин.
45. При проверке 20000 штук поршневых колец 200 штук оказались забракованными. Определите величину дисперсии доли.
46. Дисперсия признака равна 270400, коэффициент вариации равен 40,0%. Средняя величина признака равна:
47. Для оценки степени тесноты связи между уровнем выработки рабочих и стажем их непрерывной работы была рассчитана величина корреляционного отношения, оказавшаяся равной 0,9.
Учитывая, что общая дисперсия выработки рабочих составила 7,4, межгрупповая дисперсия равна
48. Если группировочный признак атрибутивный, то число групп при определяется:
1) числом его градаций;
2) числом наблюдений;
3) по формуле Стерджесса;
4) разностью между максимальным и минимальным значением группировочного признака.
49. Относительной величиной структуры является:
1) обеспеченность населения жилой площадью (м²/чел);
2) количество браков на 1000 жителей;
3) удельный вес мужчин в общей численности населения.
50. Администрация предприятия планирует сократить численность работников предприятия на 20 %, а уровень средней заработной платы работников фирмы увеличить в на 10%. Тогда фонд оплаты труда:
Источник
Задания по статистике по структурным средним
К структурным средним относятся медиана и мода.
Задача №1 . Нахождение моды и медианы для интервального ряда
Рассчитать моду по данным таблицы. Решение приведем ниже. Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10. Таким образом, получаем:
Группы предприятий по стоимости ОПФ, у.е.
1) По максимальной частоте найдем модальный интервал: Fmax =10 → I = 18-20
2) По соответствующей формуле (формулы моды и медианы приведены ниже)
Мода =18+2(10-6)/(10-6)(10-4)=18,33 млн. руб. – наиболее часто встречающаяся стоимость ОПФ среди 25 предприятий.
Вычислим медиану по приведенным исходным данным.
Как найти медиану? В данной задачи нам даны интервалы.
1) Найдем медианный интервал по накопленной частоте. Нужная накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n +1/2 или n / 2 .
Для нечетного ряда (25+1)/2= 13→ S = 18 →18-20- медианный интервал.
2) По соответствующей формуле (формулы моды и медианы приведены ниже)
Медиана Ме =18+2[(25+1)/2 — 8/10]=18,9 млн.руб. Из 25 малых предприятий региона 12 пр. имеют стоимость ОПФ менее 18 млн.руб., а 12 пр. более.
Задача №2. Нахождение моды и медианы для дискретного ряда.
тарифный разряд, Xi
Распределение рабочих 5 участков по их квалификации (тарифному разряду)
Найти моду по приведенным данным .
По максимальной частоте найдем соответствующую группу и варианту: f max=8 → Мода=4 разряд. Наиболее часто встречающийся разряд рабочих 4.
Определить медиану по данным таблицы.
Как рассчитать медиану? Прежде всего найдем медианный интервал по накопленной частоте. Нужная накопленную частоту. Накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n +1/2 или n /2.
Для четного ряда 20/2= 10→ S = 14 → Ме =4 разряд. Половина всех рабочих имеет тарифный разряд меньше 4, другая половина больше 4.
Теория для решения данных задач. Формулы для расчета моды и медианы
Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Распределительные средние – мода и медиана, их сущность и способы исчисления.
Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.
Мода 
– это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:
где: 
— нижняя граница модального интервала;
— величина модального интервала;
— частота модального интервала;
— частота интервала, предшествующего модальному;
— частота интервала, следующего за модальным;
Медиана (Ме) — это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:
где: — нижняя граница медианного интервала;
— величина медианного интервала;
— накопленная частота интервала, предшествующего медианному;
— частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Источник